Fractals are a type of mathematical object that are characterized by their self-similarity, meaning that their shape and structure are repeated at different scales. The term “fractal” was first introduced by the French mathematician Benoit Mandelbrot in 1975, and since then, fractals have become an important tool for studying complex systems and patterns in nature.
The history of fractals can be traced back to the late 19th century, when the French mathematician Gaston Julia first studied the properties of complex functions. However, it was not until the 1970s that the concept of fractals was fully developed and recognized as a distinct field of mathematics.
One of the most famous examples of fractals is the Mandelbrot set, named after its discoverer Benoit Mandelbrot. The Mandelbrot set is a complex mathematical object that can be represented graphically, and its intricate patterns have been studied by mathematicians and scientists for decades. Other well-known examples of fractals include the Sierpinski triangle, the Koch snowflake, and the dragon curve.
The astonishing images generated of fractals are a result of the process of iterating mathematical functions. By iterating a function over and over again, starting from a simple seed value, complex patterns can be generated that resemble the shapes and structures found in nature. These images are often striking and beautiful, and they have captured the imagination of mathematicians and the general public alike.
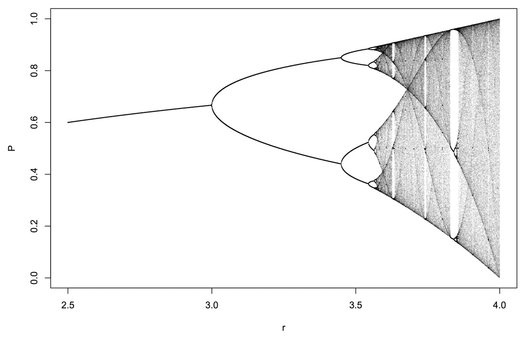
Divergence and bifurcation are two important concepts in the study of fractals. Divergence refers to the phenomenon in which a system becomes increasingly complex and less predictable over time. Bifurcation, on the other hand, refers to the splitting of a system into two or more separate components. These concepts are closely related to fractals, as they often occur in complex systems that exhibit fractal-like behavior.
Fractal dynamics refer to the behavior of complex systems that exhibit self-similar patterns at different scales. When a system behaves like a fractal, it is said to exhibit fractal dynamics. This means that its behavior can be modeled and studied using fractal mathematics, which has important implications for a wide range of fields, including physics, biology, and economics.
Finally, fractals reveal a great deal about reality, as they help us understand the underlying patterns and structures of complex systems. For example, by studying fractals, scientists have been able to gain insight into the behavior of financial markets, the spread of disease, and the growth of plants and animals. By doing so, fractals have opened up new avenues for research and helped us to better understand the world around us.
In conclusion, fractals are a type of mathematical object that are characterized by their self-similarity. The history of fractals dates back to the late 19th century, and since then, they have become an important tool for studying complex systems and patterns in nature. The images generated of fractals are a result of the process of iterating mathematical functions, and they reveal a great deal about reality. By studying fractal dynamics and the concepts of divergence and bifurcation, we can gain insight into the behavior of complex systems and better understand the world around us.